航空機の設計について3;概念設計その2
記事の説明
この記事シリーズは、航空機の専門書として有名な"Aircraft Design A Systems Engineering Approach"の中で、整理したい箇所をまとめた備忘録です。機体の設計について学んでいると「この計算は設計のどの段階で行うものなのか?」と迷うことがあります。このような自分の為に整理したメモをこのシリーズで書いていきます。
この記事は第3章の内容を参考にしています。
目次
機体構成の選択とトレードオフ
前回の記事では、機体構成の選択肢について説明しました。選択肢が多くないといえ、要求に対し最適な構成を選択するにはある程度の指標が必要です。構成要素の採用したい良い点、出来るだけ抑え込みたい悪い点をバランスよく取り入れる為、トレードオフ分析が行われます。
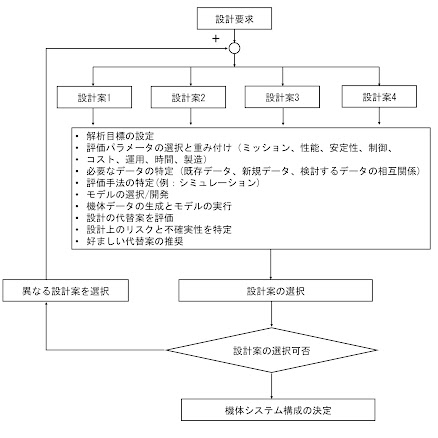
トレードオフ分析の対象としては、前回記事で示したような要素だけでなく材料、製造プロセス、部品や材料の調達先まで及びます。このプロセスを模式図で示したものを下に示します。
この図の真ん中で示した(解析目標の設定~好ましい代替案)の推奨のプロセスで、設計案の中から選択が行われます。旅客機の設計では、この過程で多分野統合最適化:Multi-Disciplinary Optimization [MDO]が採用される事があります。MDOは、最適化手法を用いて、多くの分野を含む設計問題を解決する設計手法の一つです。各分野を逐次最適化して最適解を導く方法とは異なり、設計に含まれるすべての分野を関係性(本では相互作用)を考慮して設計する事が可能です。
B787で採用されたケース(エコな航空機を実現するための空力技術)や、MRJ計画で採用されたケース(環境適応型高性能小型航空機設計における~)が存在します。
設計者の定める優先度
設計者は設計の過程において、様々な優先順位を持っています。これらの優先順位は、設計する機体に要求される仕様で変化します。優先度が変化する例を下の表で示します。
この優先度はこの本(Aircraft Design A Systems Engineering Approach)の著者によって決められたものなので、あくまで一例として捉えてください。主に10項目で分けられており、製造コスト、性能、飛行性能、設計期間、美しさ(民間機)、美しさ(軍用機)、整備性、生産性、機体重量、廃棄性、ステルス性で分けられています。この表中では10個の長所(基準)の中で、等級「1」が最も優先度が高く、等級「10」が最も優先度が低くなってます。等級「0」は、その項目が考慮にいれる基準でないことを意味します。
機種ごとに優先度が定まっていたとしても、設計者によって重みを置く割合は異なります。例として戦闘機を設計する際、設計者によって利点の重みづけが異なる事を以下の表で示します。
概念設計の最適化
ここからは概念設計の最適化について説明していきます。大まかにいえば、
- 設計で求められる設計要件を数値で表す目的関数があり
- その目的関数を最大もしくは最小化する数値(機体の構成要素に関する数値)を求める
という手順を指します。
数学的ツール
ここからは設計における最適化の話をしたいのですが、その前に数学的な意味の話が必要です。この話が分かる方は「数学的ツール」の項目は読み飛ばしても構いません。
単一目的最適化問題
数学における最適化とは、目的関数と呼ばれる関数の最適値(最大値または最小値)を、変数に設定された制約条件のもとで決定する問題です。まず、最適化問題を目的関数と制約条件によって記述する必要があります。
最適化問題の基礎として、一つの目的関数に対する最適化を説明します。
最適化とは目的関数の値最小化(場合によっては最大化)するように引数を選ぶ事を意味します。目的関数が3次関数であるとき、これを数式で表すと
\begin{align}
minimize \; f(x)=5x^3-10x\qquad where -1 \leq x \leq 1
\end{align}
これはf(x)を$-1 \leq x \leq 1$の条件化(範囲で)最小化せよという意味です。
この時xの受ける条件を「制約条件」といいます。この場合$x=1$が目的関数を最小化する$x$は$x=1$です。とても簡単な例ですが、これも最適化の作業です。本来の設計ではこの目的関数が設計しているシステムの一部を反映しています。
少しだけ言い方を一般化しましょう。
\begin{align}
minimize \; f(x) where\; \mathrm{x} \in \mathrm{R}^{\mathrm{n}}
\end{align}
「関数$f(x)$を$\mathrm{R}^{\mathrm{n}}$という条件で最小化せよ」という意味になります。$\mathrm{R}^{\mathrm{n}}$はn次元のユークリッド空間という意味です。ユークリッド空間の意味について参考になりそうなサイトとしては、以下のサイトが分かりやすかったです。
最適化のプロセスでは「目的関数がn個の変数をもつ」または「目的関数がnの変数を持つ実数の集まり」と言い換えられると思われます。
さらに一般化しましょう。
\begin{align}
optimize \; f(x) subject\;to\; \mathrm{x} \in \Omega
\end{align}
ここで、関数$f(x)$はn個の実数を持ち、$\mathrm{R}^{\mathrm{n}}$を集合とみなすと$x$は$\mathrm{R}^{\mathrm{n}}$の要素です。このとき関数$f$はx次元のベクトルとして表すことができ、\begin{align}x=\left[x_1, x_2, \ldots, x_n\right]^T \in R^n\end{align}
なお$Omega$は$\mathrm{R}^{\mathrm{n}}$の部分集合です。
多目的最適化問題
実際の設計では目的関数が単一という事はありません。設計における構成部品やシステムが増えれば増えるほど、目的関数の数は増えます。一般に多目的最適化問題は
- 全ての目的関数を最小化する
- 全ての目的関数を最大化する
- 一部の関数を最小化、他の関数を最大化する
上記をまとめて式で表すと \begin{align} minimum\;f(x)\;= \;maximum \;[-f(x)]\end{align}
この問題を単一目的最適化問題に変換する方法があります。変換する一つの方法が、目的関数ベクトル
\begin{align}f(x)=\left[f_1(x),f_2(x), \ldots,,f_l(x)\right]^T \end{align}
の成分を正の係数で線形結合して単一の目的関数を形成する事です。これを数学用語を使って言い表すと、目的関数の要素を「凸結合する」といいます。凸結合とは掛け合わす係数が正の値であり、その和が1となるような線形結合の事を指します。この線形結合を式で表すと、
\begin{align}F(x)=c^T \quad f(x)\end{align}
ここで$c$は正の成分を持つベクトルです。
このように複数の目的関数(もしくは目的関数の出力)を線形結合しつつ、設計要求に基づいた重みづけをする事で、設計する機体を要求される仕様や性能に近付けていきます。
最適化の手順と方法
直前の項目の「数学的ツール」では概念設計の最適化で使用される数学(算数?)の説明をしました。ここからはその手順をより具体的に示していきます。
1.設計での優先順位を決める
まずは設計での優先順位を決めます。「設計者の定める優先度」で示した表を再度示します。後の計算に使用する為、これらの優先度に記号を振り分けます。
$P_{\mathrm{i}}$は$i$の内容の設計における割合(優先度)を表しています。上の表を詳しく説明すると、
- $P_{\mathrm{C}}$;コストの重視する割合(Percentage of cost)
- $P_{\mathrm{F}}$;機能を重視する割合(Percentage of function)
- $P_{\mathrm{P}}$;飛行性能を重視する割合(Percentage of performance)
- $P_{\mathrm{T}}$;設計期間を重視する割合(Percentage of time)
- $P_{\mathrm{B}}$;見た目(軍用機では怖さ?)を重視する割合(Percentage of beauty)
- $P_{\mathrm{M}}$;整備性を重視する割合(Percentage of maintainability)
- $P_{\mathrm{R}}$;製造効率を重視する割合(Percentage of ? )
- $P_{\mathrm{W}}$;軽量化を重視する割合(Percentage of weight )
- $P_{\mathrm{D}}$;廃棄のし易さを重視する割合(Percentage of disposability )
- $P_{\mathrm{S}}$;ステルス性を重視する割合(Percentage of stealthiness)
例えば設計の過程において、低コスト化を重視する割合を8%である場合は、$P_{\mathrm{C}}=0.08$となるわけです。何をもってその割合を計算するかは人それぞれですが、その検討に掛ける時間や人工、単に概念設計を担当する設計者が重視する割合(なんとなく)等さまざまかと思われます。
2.設計要素毎に、基準指数を決定する
1.で決定した設計における割合(優先度)を基に、機体の構成要素(主翼、胴体、脚等細かく出来るなら出来るだけ...)に点数をつけていきます。
この表ではランディングギアのコスト~廃棄性のそれぞれについて点数を付けたものです。
左端の記号は、次の項目で使用します。
3.基準指数毎に足し合わせる
同様に構成要素毎にコスト、機能、飛行性能、設計期間、見た目、整備性、生産性、機体重量、廃棄性、ステルス性毎に点数を振ったものを足し合わせます。上の表でランディングギアの基準指数が$x_{C_1}$等と表されるのは、ランディングギアを一番目の構成要素としたためであり、主翼が1番目でもどのような順番でもいいです。とにかく考えられる構成要素の全てで2.のように基準指数を決め、足し合わせる事が出来ればよいのです。
\begin{align}{CI}=\sum_{i=1}^{k} x_{C_i}\end{align}
\begin{align}{PI}=\sum_{i=1}^{k} x_{P_i}\end{align}
\begin{align}{FI}=\sum_{i=1}^{k} x_{F_i}\end{align}
\begin{align}{TI}=\sum_{i=1}^{k} x_{T_i}\end{align}
\begin{align}{BI}=\sum_{i=1}^{k} x_{B_i}\end{align}
\begin{align}{MI}=\sum_{i=1}^{k} x_{M_i}\end{align}
\begin{align}{RI}=\sum_{i=1}^{k} x_{R_i}\end{align}
\begin{align}{WI}=\sum_{i=1}^{k} x_{W_i}\end{align}
\begin{align}{DI}=\sum_{i=1}^{k} x_{D_i}\end{align}
\begin{align}{SI}=\sum_{i=1}^{k} x_{S_i}\end{align}
4.二つの設計指標($\mathrm{DI}_{\min }$,$\mathrm{DI}_{\max }$)と設計の優先順位($\mathrm{P}_{\min }$,$\mathrm{P}_{\max }$)を計算する
式(8)から式(17)の中で値が小さい方が良いのは、${CI}$,${WI}$,${TI}$の3つであり、残りの結果は大きい方が良いと見なせます。これまで説明した1.,2.と3.から、小さくなって欲しい値をまとめると
\begin{align}\mathrm{DI}_{\min }=\mathrm{CI} \cdot P_{\mathrm{C}}+\mathrm{WI} \cdot P_{\mathrm{W}}+\mathrm{TI} \cdot P_{\mathrm{T}}\end{align}
大きくなって欲しい値をまとめると、
\begin{align}\mathrm{DI}_{\max }=\mathrm{PI} \cdot P_{\mathrm{P}}+\mathrm{FI} \cdot P_{\mathrm{F}}+\mathrm{BI} \cdot P_{\mathrm{B}}+\mathrm{MI} \cdot P_{\mathrm{M}}+\mathrm{RI} \cdot P_{\mathrm{R}}+\mathrm{DI} \cdot P_{\mathrm{D}}+\mathrm{SI} \cdot P_{\mathrm{S}}\end{align}
また、1.で定めた優先度の内小さくなって欲しいモノの割合の和は
\begin{align}P_{\min}=P_{\mathrm{C}}+P_{\mathrm{W}}+P_{\mathrm{T}}\end{align}
大きくなって欲しいモノの割合の和は
\begin{align}P_{\max}=P_{\mathrm{P}}+P_{\mathrm{F}}+P_{\mathrm{B}}+P_{\mathrm{M}}+P_{\mathrm{R}}+P_{\mathrm{D}}+P_{\mathrm{S}}\end{align}
5.設計指標と設計の優先順位を基に、望ましい設計案を採用する
最適な設計指標をもたらす構成は、最終的に2つに絞られます。一つは最も低い$\mathrm{DI}_{\min }$をもたらす構成、もう一つは最も高い$\mathrm{DI}_{\max}$をもたらす構成です。
ではどちらを選べば良いかというと、$P_{\min}$が$P_{\max}$より大きい場合は,${DI}_{\min}$が最も小さい構成が最適な構成として選択されます。${P}_{\min}$より${P}_{\max}$の方が大きい場合は,${DI}_{\max}$が最も高くなるように設定する。PminとPmaxの差があまりない場合(例えば51%と49%)となる場合には、設計における要求や実際の運用を考慮して決めていく必要があります。(翻訳元の本では''システムエンジニアリングの手順を踏む必要がある''との記載あり)







コメント
コメントを投稿